[문제풀이] 사탕 상자

1. 설명

사탕 상자

문제

수정이는 어린 동생을 달래기 위해서 사탕을 사용한다. 수정이는 평소에 여러 개의 사탕을 사서 사탕상자에 넣어두고, 동생이 말을 잘 들을 때면 그 안에서 사탕을 꺼내서 주곤 한다.

각각의 사탕은 그 맛의 좋고 나쁨이 1부터 1,000,000까지의 정수로 구분된다. 1이 가장 맛있는 사탕을 의미하며, 1,000,000은 가장 맛없는 사탕을 의미한다. 수정이는 동생이 말을 잘 들은 정도에 따라서, 사탕상자 안에 있는 사탕들 중 몇 번째로 맛있는 사탕을 꺼내주곤 한다. 예를 들어 말을 매우 잘 들었을 때에는 사탕상자에서 가장 맛있는 사탕을 꺼내주고, 말을 조금 잘 들었을 때에는 사탕상자에서 여섯 번째로 맛있는 사탕을 꺼내주는 식이다.

수정이가 보관하고 있는 사탕은 매우 많기 때문에 매번 사탕상자를 뒤져서 꺼낼 사탕을 골라내는 일은 매우 어렵다. 수정이를 도와주는 프로그램을 작성하시오.

입력

첫째 줄에 수정이가 사탕상자에 손을 댄 횟수 n(1≤n≤100,000)이 주어진다. 다음 n개의 줄에는 두 정수 A, B, 혹은 세 정수 A, B, C가 주어진다. A가 1인 경우는 사탕상자에서 사탕을 꺼내는 경우이다. 이때에는 한 정수만 주어지며, B는 꺼낼 사탕의 순위를 의미한다. 이 경우 사탕상자에서 한 개의 사탕이 꺼내지게 된다. 또, A가 2인 경우는 사탕을 넣는 경우이다. 이때에는 두 정수가 주어지는데, B는 넣을 사탕의 맛을 나타내는 정수이고 C는 그러한 사탕의 개수이다. C가 양수일 경우에는 사탕을 넣는 경우이고, 음수일 경우에는 빼는 경우이다. 맨 처음에는 빈 사탕상자에서 시작한다고 가정하며, 사탕의 총 개수는 2,000,000,000을 넘지 않는다. 또한 없는 사탕을 꺼내는 경우와 같은 잘못된 입력은 주어지지 않는다.

출력

A가 1인 모든 입력에 대해서, 꺼낼 사탕의 맛의 번호를 출력한다. 물론, A=2 이면서 C<0 일 때는 출력하지 않는다.

입력예제

6
2 1 2
2 3 3
1 2
1 2
2 1 -1
1 2

출력예제

1
3
3

2. 문제풀이

처음에 이문제를 봤을 때, 세그먼트 트리로 어떻게 풀어야 할지 막막했습니다. 그런데, 생각해보면, 세그먼트 트리에 사탕의 갯수에 맞춰서 트리를 구성합니다. 상위부터 계속해서 체크를 하면서 K번재의 갯수가 있으면, 그만큼 빼주고, 다시 우측으로 가서 K-tree[node]만큼을 계산해서 몇번째인지를 찾게 됩니다.

그림으로 설명을 드리겠습니다.

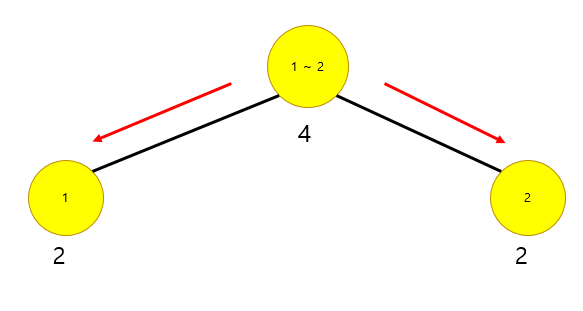
위의 예에서 3번째의 숫자를 찾는다고 가정을 해봅시다. 루트노드부터 훑어서 내려오게 됩니다.

public static long query(int node, int start, int end, int k){
        if(start == end){
            System.out.println(start + " ");
            return start;
        }
        if(node *2 <= tree_size && tree[node * 2] >= k){
            return ret = query(node *2, start, (start + end) / 2, k);
        }
        k -= tree[node * 2];
        if(node * 2 + 1 <= tree_size && tree[node * 2 + 1] >= k){
            return ret = query(node * 2 + 1, (start + end) / 2 + 1, end, k);
        }
        return 0;
    }

위의 코드에서 보면, 재귀 형식으로 짜여져 있습니다. 이전의 세그먼트 트리에서의 구조와 유사합니다. 하지만, child node로 내려가는 조건이 tree[node * 2]와 같이 특정 값이 인풋으로 온 k보다 크거나 같을때 내려가도록 되어있습니다.

위의 예시에서는 3번째인 수를 찾을때는 루트 노드(4) >= 3번째가 성립하기 때문에, 아래의 Child Node로 내려가게 됩니다. 그리고 재귀형식으로 범위를 좁혀가면서 호출을 하게 되는 구조입니다.

그러다가 좌측보다 K번째가 큰 경우가 생기게 되면 다음이 수행됩니다.

k -= tree[node * 2];

k – tree[node * 2]를 k로 업데이트를 해줍니다. 위의 예에서는 좌측의 child node(2)와 k번쨰(3)를 보게 되면 k가 크기 때문에 2를 빼준 1을 오른쪽 노드에서 찾게 됩니다.

if(node * 2 + 1 <= tree_size && tree[node * 2 + 1] >= k){
    return ret = query(node * 2 + 1, (start + end) / 2 + 1, end, k);
}

오른쪽 노드도 역시 tree[node * 2 +1]값이 k번째보다 큰지 체크를 하고 같은 방식으로 아래로 내려가게 됩니다.

if(start == end){
    System.out.println(start + " ");
    return start;
}

끝으로, 말단 노드(Leaf)까지 내려오게 되면, 해당 index값을 return해주게 됨으로써 k번째 수의 위치를 반환하게 됩니다.

이후에는 반환된 노드에 대해서 -1로 업데이트를 수행하게 됩니다. 이부분이 사탕을 뺴어주는 내용입니다.

풀이

import java.io.*;
import java.util.StringTokenizer;

public class segment_2243 {
    static long[] tree;
    static long[] arr;
    static int N,tree_size;
    static StringTokenizer st;
    static long ret;
    public static void update(int node, int start, int end, int index, long diff){
        if(!(start <= index && index <= end)) return;
        tree[node] += diff;
        if(start != end){
            int mid = (start + end ) >> 1;
            update(node * 2, start, mid, index, diff);
            update(node * 2 + 1, mid + 1, end, index, diff);
        }
    }
    public static long query(int node, int start, int end, int k){
        if(start == end){
            System.out.println(start + " ");
            return start;
        }
        if(node *2 <= tree_size && tree[node * 2] >= k){
            return ret = query(node *2, start, (start + end) / 2, k);
        }
        k -= tree[node * 2];
        if(node * 2 + 1 <= tree_size && tree[node * 2 + 1] >= k){
            return ret = query(node * 2 + 1, (start + end) / 2 + 1, end, k);
        }
        return 0;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        int h = (int)Math.ceil(Math.log(1000000) / Math.log(2));
        tree_size = 1 << h + 1;
        tree = new long[tree_size];
        arr = new long[N + 1];
        for (int i = 0; i < N ; i++) {
            int A,B,C;
            st = new StringTokenizer(br.readLine());
            A =  Integer.parseInt(st.nextToken());
            if(A == 1){
                B = Integer.parseInt(st.nextToken());
                int getIndex = (int) query(1, 0,  1000000, B);
                update(1, 0, 1000000, getIndex, -1);
            }
            else if(A == 2){
                B = Integer.parseInt(st.nextToken());
                C = Integer.parseInt(st.nextToken());
                update(1, 0, 1000000, B, C);
            }
        }
    }
}