[Algorithms] LCA 알고리즘
[Algorithms] LCA 알고리즘
안녕하세요? 정리하는 개발자 워니즈입니다. 이번시간에는 이진트리에서 최저 공통 조상을 찾아나가는 알고리즘인 LCA(Lowest Common Ancestor) 알고리즘에 대해서 정리를 해보도록 하겠습니다.
LCA 알고리즘은 최소 공통 조상을 찾는 알고리즘이고, 트리의 두 노드로부터 최적의 공통 노드를 찾아 나가는 알고리즘입니다.
1. LCA 알고리즘 원리
공통 조상을 찾기 위해서는 다음과 같은 트리가 있다고 가정합니다.
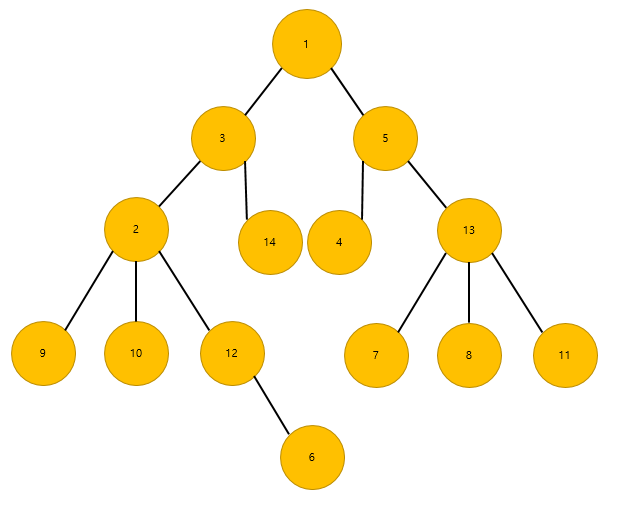
1번 노드가 최상위 루트 노드이고, 밑으로 child들이 달린 트리로 구성이 되어있습니다.
여기서 LCA(14, 7)을 요청하게 되면, 어떤값이 나올까요? 답은 1입니다.
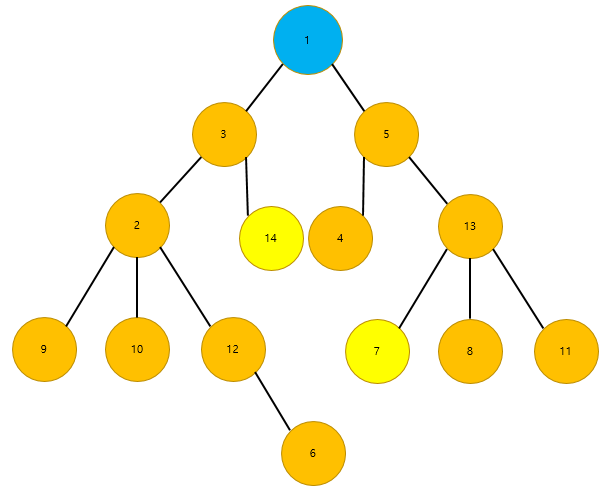
그렇다면, LCA(9, 10)은 무엇일까요? 답은 2입니다
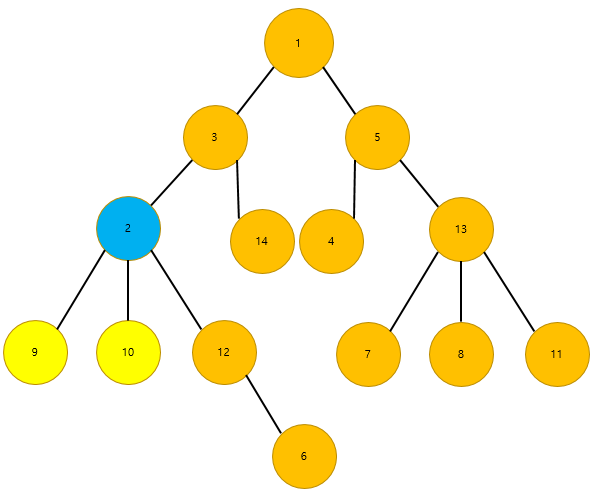
LCA(12, 6)은 무엇일까요? 답은 12입니다.
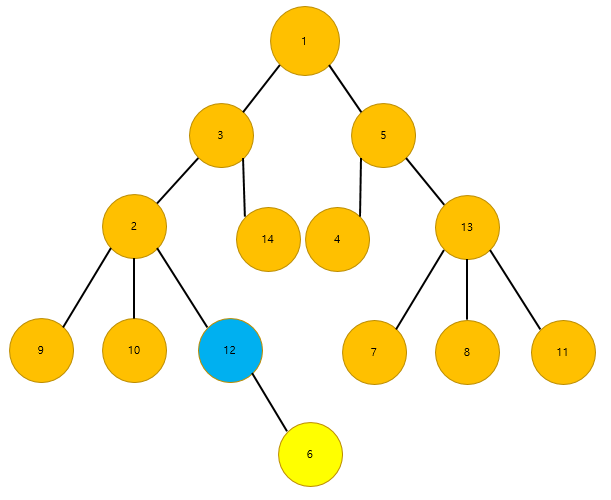
이제 공통 조상에 대한 감이 오시나요? 위로 거슬러 올라가면서 만날 수 있는 최단의 노드가 공통조상이 됩니다.
알고리즘을 이해하기 위해서는 DP식을 이해해야합니다. LCA같은 경우는 input이 양방향으로 들어오게 됩니다. 그리고 depth와 parent배열을 이용해서 다음과 같은 모습으로 트리를 구성하게 되빈다.
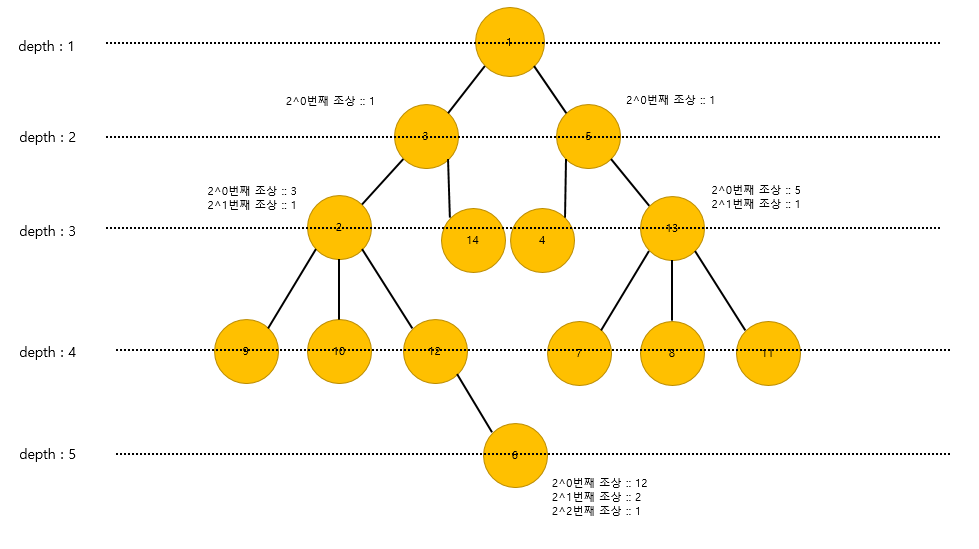
이떄 parent배열은 parent[ i ] [ k ]와 같이 채워지게 되는데, i의 2^k번째 노드의 값이 채워지게 됩니다.
LCA는 이러한 2^k번째를 이용해서 훨씬 빠르게 노드를 검색하게 됩니다. 공통 조상을 구해나가는 알고리즘의 흐름은 다음과 같습니다.
- 두 노드간의 depth가 더 깊은 것을 동일 선상으로 맞추는 작업
- 조상배열을 통해서 공통의 조상 바로 밑까지 올리는 작업
예를들어 LCA(5, 6)을 수행한다고 가정합니다. 아래그림처럼 6의 노드가 depth가 더 깊기때문에 5의 depth까지 맞추는 작업을 수행해야합니다. 하지만, parent는 2^k로 위로 거슬러 올라가기때문에 2^2번째가 되게 되면, 5번 노드보다 값이 더 작아지게 됩니다.
그래서 1차로는 2^1번째 노드인 2번 노드까지 올리게됩니다.
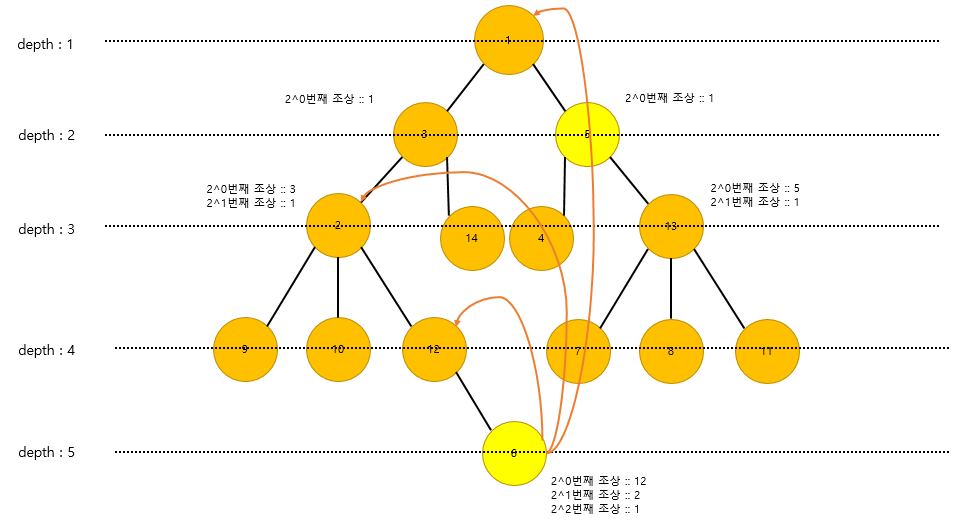
그리고 나서 2번 노드에서 다시 parent배열을 통해서 2^0번번째인 depth 2까지 올리게 됩니다.
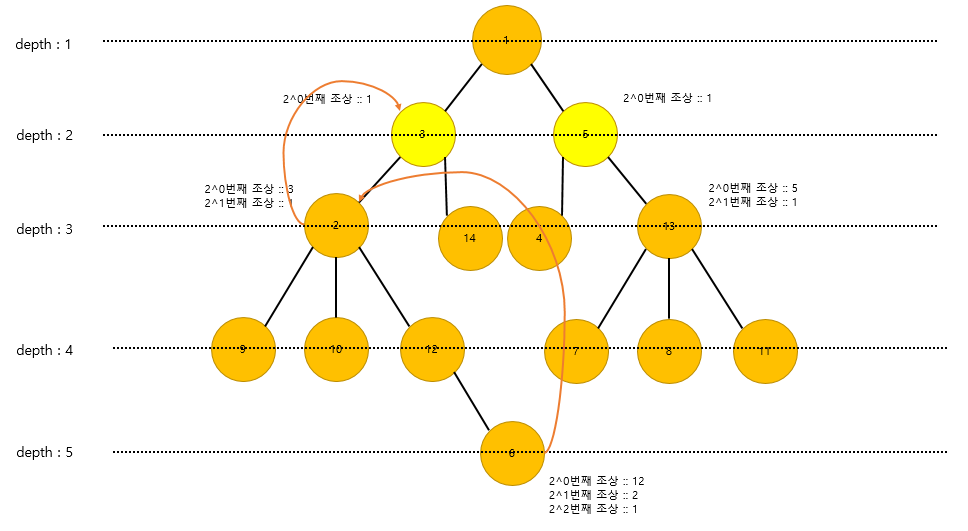
그리고 나서, 최종적으로 같은 depth로부터 위로 찾아나가면서 공통적인 노드를 반환합니다. 이것이 바로, LCA를 구하는 알고리즘의 동작 방식입니다.
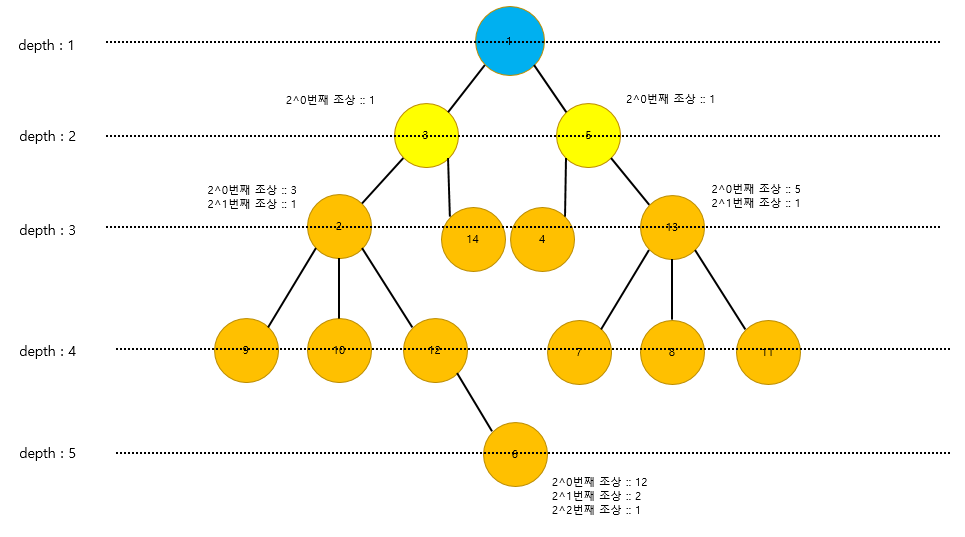
2. 초기화 과정
LCA 알고리즘에서 필요한 변수는 크게 다음과 같습니다.
- parent : 2차원 배열로 선언하여, i의 2^K번째 노드를 찾아나갈 때 사용하는 변수 입니다.
- ad : 필자 같은 경우 인접리스트를 ArryList안에 ArrayList로 구현을 했습니다.
- depth : 1차원 배열로 현재 노드의 depth를 타나내는 변수입니다.
2-1. BFS를 활용한 초기 parent 구성
c[1] = 1;
q.add(1);
while(!q.isEmpty()){
int x = q.poll();
for (int i = 0; i < ad.get(x).size(); i++) {
int to = ad.get(x).get(i);
int y = to;
if(c[y] == 0){
depth[y] = depth[x] + 1;
parent[y][0] = x;
c[y] = 1;
q.add(y);
}
}
}
2-2. DP를 활용한 parent 구성
for (int k = 1; k < 17; k++)for (int i = 1; i <= n; i++) {
parent[i][k] = parent[parent[i][k-1]][k-1];
}
3. 공통 조상 쿼리 과정
공통 조상을 쿼리하는 방식은 위에서 설명했다시피, 두개 노드중에서 depth가 더 깊은것을 동일 선상으로 올리는 작업을 1차적으로 수행합니다.
//depth를 항상 u가 더 깊게 하기 위해서 swap
if(depth[u] < depth[v]){
int temp;
temp = u;
u = v;
v = temp;
}
int diff = depth[u] - depth[v];
//두 노드간의 depth차이 만큼 u를 맞춰주는 작업을 수행합니다.
for (int k = 0; diff != 0; k++) {
if((diff & 1 )== 1) u = parent[u][k];
diff >>= 1;
}
//두개가 동일하다면 u를 반환합니다.
if(u == v) return u;
2개의 노드가 동일 선상으로 맞춰졌다면, parent 배열로부터 2개의 노드가 달라지는 위치로 계속해서 노드를 업데이트 해줍니다. 그렇게 되면, 17번의 for문이 모두 돌고 나면, 공통조상의 마래 아래 depth의 노드까지 올라온것을 확인 할 수 있습니다.
for (int k = 17; k >= 0; k--) {
if(parent[u][k]!= parent[v][k]){
u = parent[u][k];
v = parent[v][k];
}
}
return parent[u][0];
