[Algorithms] 세그먼트 트리
[Algorithms] 세그먼트 트리
안녕하세요? 정리하는 개발자 워니즈입니다. 이번시간에는 알고리즘 자료구조중 가장 많은 활용도를 보이는 세그먼트 트리에 대해서 정리를 해보도록 하겠습니다.
세그먼트 트리는 여러개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 방법에 관한 것입니다. 예를들어, 배열에 1 2 3 4 5 라는 내용이 들어있다고 가정합니다. 배열의 이름은 arr이고, index의 시작은 1이라고 가정합니다.
2번째 부터 5번째의 구간의 수를 더하라고 가정을 하면, 쿼리는 arr[2] + arr[3] + arr[4] + arr[5]가 될 것입니다. 여기서 다시 3번째 수를 6으로 변경하고, 더하는 수를 다시 구하면, 쿼리는 arr[2] + arr[3] + arr[4] + arr[5]가 됩니다. 변경하는 쿼리는 O(1)이지만, 합을 구하는 쿼리는 O(N)만큼이 들게 됩니다. 그리고 M번의 작업을 진행하게 되면 O(NM)만큼의 시간복잡도가 걸리게 됩니다.
1. 세그먼트 트리란?
위의 설명에서 시간복잡도 관련해서 기존 방식으로는 수가 커질수록 시간 복잡도가 많이 소모된다는 것을 알 수 있습니다.
세그먼트 트리에서는 다음과 같은 시간 복잡도를 갖습니다.
- 수를 바꾸는 과정 (O(logN))
- 수를 더하는 과정(O(logN))
- M번 수행한다고 가정하면, O(MlogN + MlogN) -> O(MlogN)이 걸리게 됩니다.
세그먼트 트리를 구성하기 위해서는 2개의 배열을 구성합니다. 실제 트리를 구성해주는 tree배열과, 인풋 정보에 대한 배열인 arr 배열을 설명합니다.
2. 초기화 과정(Init)
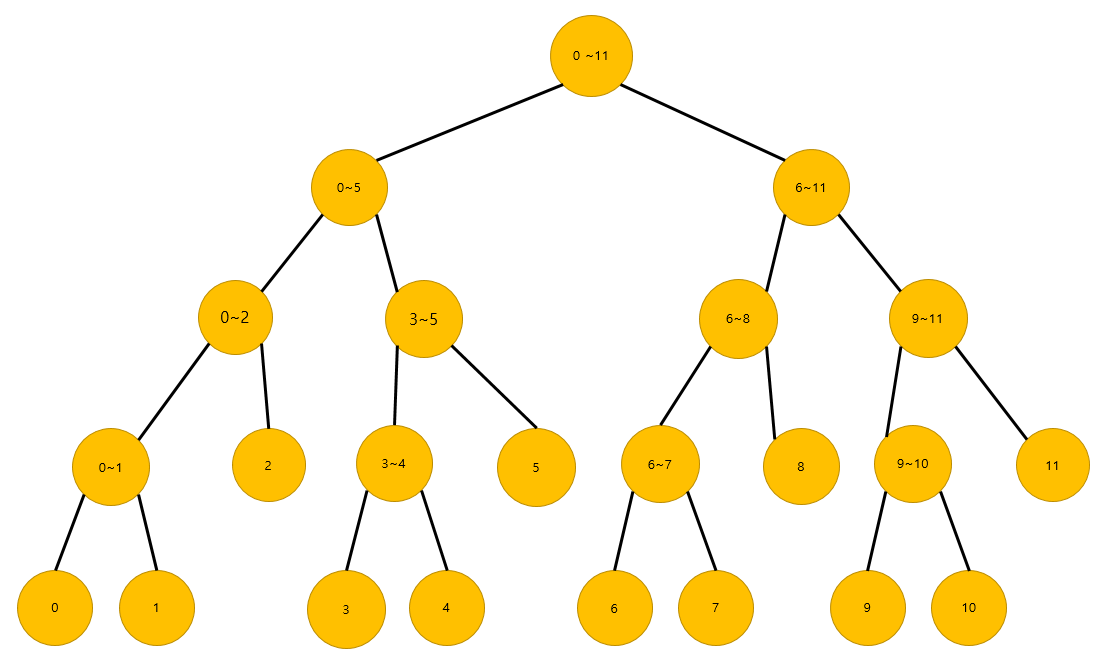
초기화라는 의미는 트리에 대한 정보를 초기 셋팅해주는 상태를 말합니다. 구간에 대한 합정보를 상위 노드가 담고 있습니다. 아래의 그림과 같은 구성이 되어집니다.
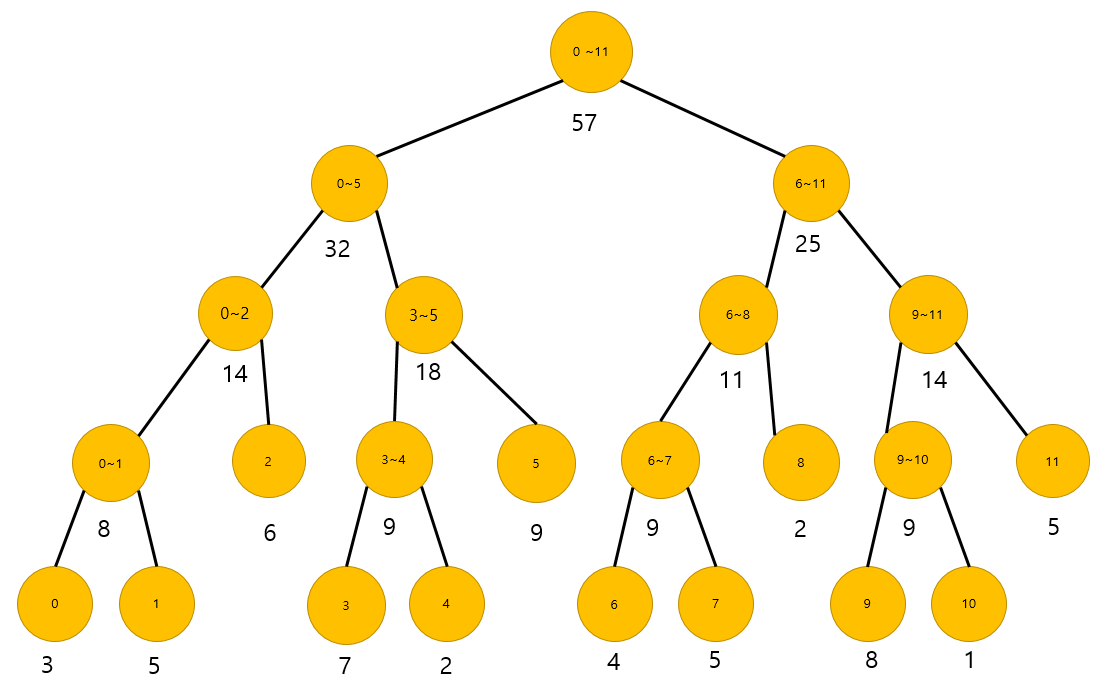
arr의 배열은 다음과 같이 구성되어있습니다.
arr = {3, 5, 6, 7, 2, 9, 4, 5, 2, 8, 1, 5}
public static long init(int node, int start, int end){
if(start == end) return tree[node] = arr[start];
int mid = (start + end) >> 1;
return tree[node] = init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end);
}
시작되는 node에 대한 정보, 그리고 start, end지점에 대해서 초기화를 거칩니다.
위의 그림을 초기화 해보겠습니다.
init(1, 0, 12);
1번의 tree Node
0 ~ N(12) 까지의 arr 배열 정보
if(start == end) return tree[node] = arr[start];
init 함수에서 위의 코드를 잘 보아야합니다. start end 가 같아지는 경우, arr[start]정보를 tree[node]지점에 넣어주게 됩니다.
트리구조는 완벽한 2진트리로 구성이 되어지고, 계속해서 child를 좌/우측 노드로 갖게 됩니다. 그래서 초기에 들어온 정보에 대해서 좌/우로 나눠져 내려가다가 말단 노드(Leaf)가 되어지면, 해당 정보를 업데이트 하게 됩니다.
재귀형식으로 구현되어있는 함수이므로, 스택이 계속해서 쌓여나가고 말단 노드부터 차곡차곡 위로 올라가면서 값을 합산하게 됩니다.
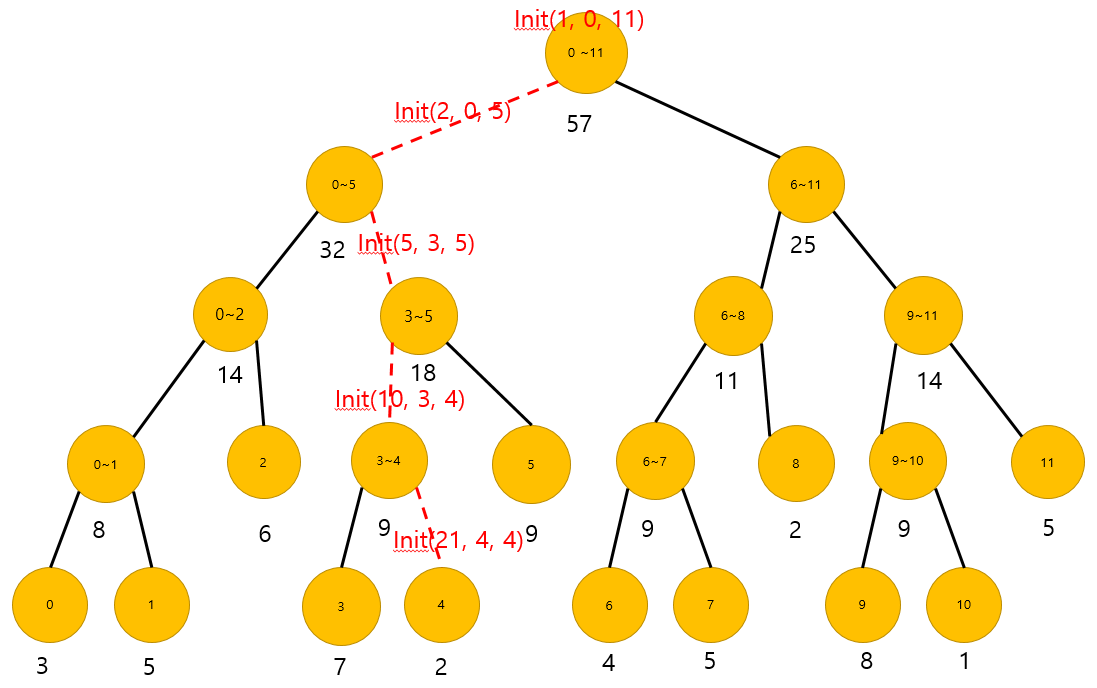
위의 그림에서 보시면, 제일 마지막 노드로 내려가서 Init(21, 4, 4)를 나타내고, start end이기 떄문에 tree[21] = arr[4]를 업데이트 하게 됩니다. 이런식으로 재귀적으로 호출을 하게되면, 위의 그림과 같이 tree의 초기값이 입력이 됩니다.
3. 갱신 과정(Update)
갱신 과정은 특정 말단 노드의 값을 A->B로 변경하는 방법에 대한 내용입니다. 아래의 그림처럼, 특정 값을 업데이트를 하게 되면, 그 상위의 관연관되어있는 부모 노드에 대해서도 값을 업데이트를 해주어야 합니다 .
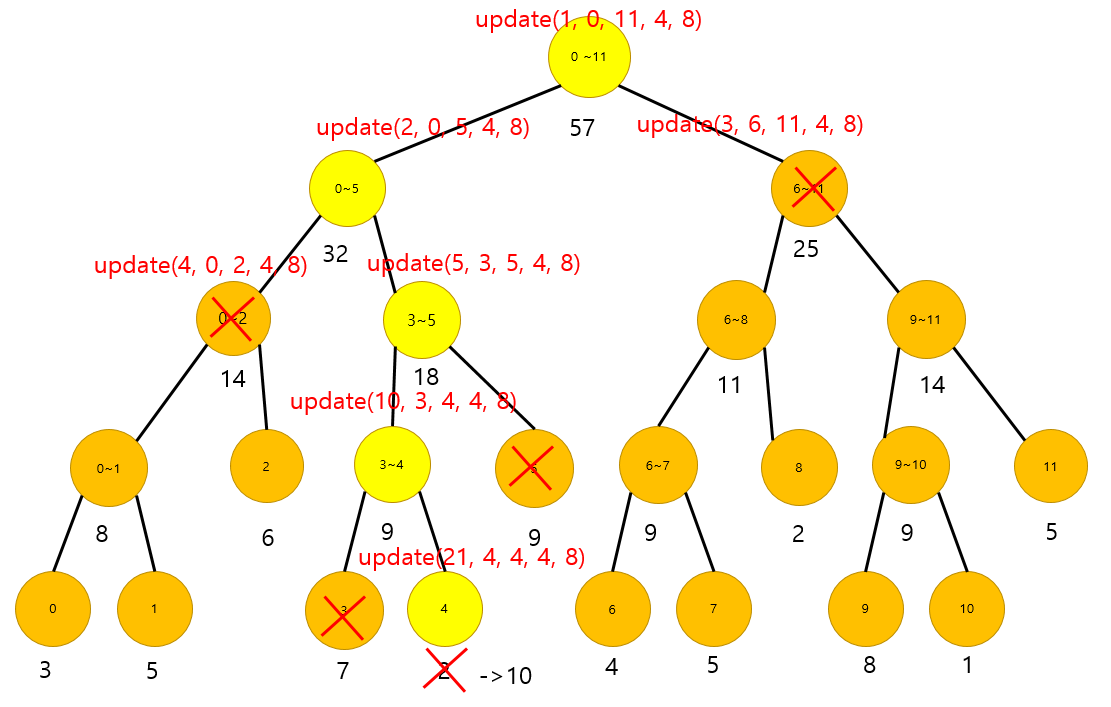
위의 그림에서 보면, arr[4] = 2였던 값을, 10으로 변경하고자 합니다. 그렇게 되면, 상위의 모든 부모 노드들에 대해서도 diff(업데이트하는 value의 차이)만큼 업데이트를 해주어야 합니다.
public static void update(int node, int start, int end, int index, long diff){
if(!(start <= index && index <= end)) return;
tree[node] += diff;
if(start != end){
int mid = (start + end) >> 1;
update(node * 2, start, mid, index, diff);
update(node * 2 + 1, mid + 1, end, index, diff);
}
}
위의 코드가 실제로 업데이트를 하는, 내용입니다.
update(1, 0, 11, 4, 8)의 의미는, tree의 1번 노드에서, 말단 노드의 0~11번 노드까지 훑으면서 4번째의 값을 8만큼의 차리로 업데이트를 해준다는 내용입니다.
역시 재귀적으로 짜여져있습니다.
if(!(start <= index && index <= end)) return;
실제 업데이트하는 index가 말단 노드사이에 없으면, return을 합니다.
tree[node] += diff;
if(start != end){
int mid = (start + end) >> 1;
update(node * 2, start, mid, index, diff);
update(node * 2 + 1, mid + 1, end, index, diff);
}
그다음의 코드는, 실제 tree의 값을 업데이트하고, 자식으로 업데이트 정보를 넘기는 내용입니다. 이런식으로 계속해서 내려가면서 정보를 업데이트를 해주게 됩니다.
4. 구간합 과정(sum)
구간합을 구하는 과정은, 크게 4가지로 생각해 볼 수 있습니다.
- left, right와 start, end가 겹치지 않는 경우
- left, right가 start, end를 완전히 포함하는 경우
- start, end가 left, right를 완전히 포함하는 경우
- left, right와 start, end가 겹치는 경우
3,4 같은 경우는 범위를 계속해서 좁히기 위해서 재탐색을 수행합니다.
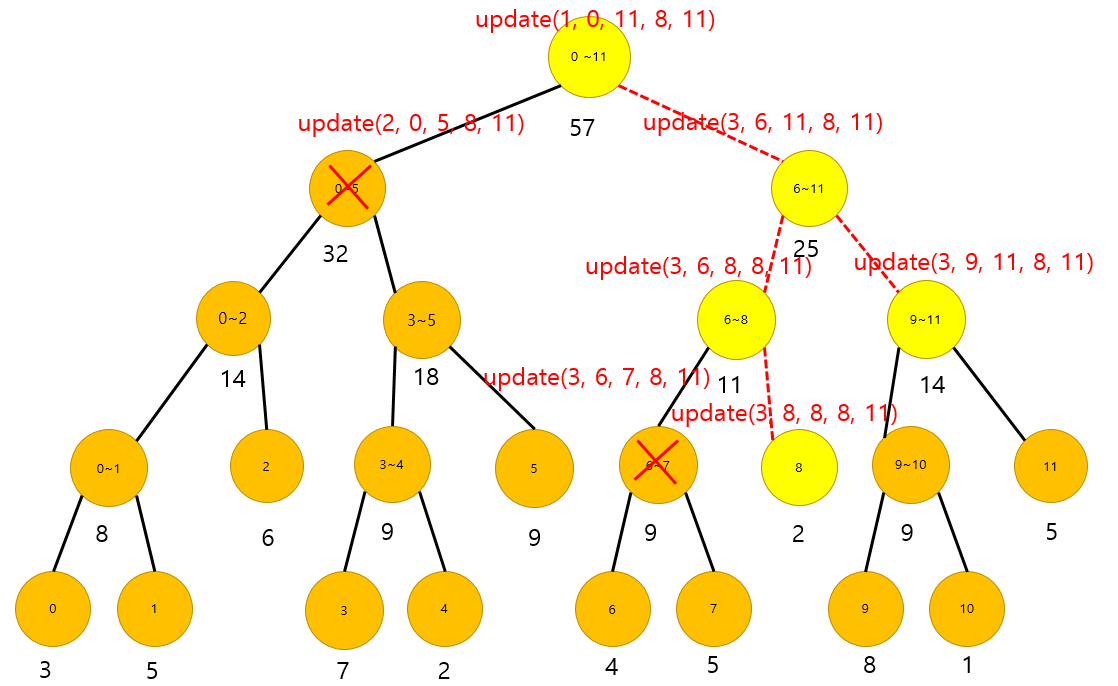
위의 그림에서 보면, 8 – 11까지의 숫자에 대한 구간합을 구하는 내용입니다.
update(1, 0, 11, 8, 11) 이고 시작하는 tree의 노드정보에 이어서, 말단 노드의 시작과 끝정보(0 ~ 11), 그리고 구간을 구하고자 하는 left와 right의 내용( 8 ~ 11 )이 파라미터로 들어가게 됩니다.
public static long sum(int node, int start, int end, int left, int right){
if(left > end || right < start) return 0; // 범위에 속하지 않으면, return
if(left <= start && end <= right) return tree[node]; // left,right가 완전히 포함하면, tree정보 리턴
//그외의 경우는 범위를 쪼갠다.
int mid = (start + end) >> 1;
return sum(node * 2, start, mid, left, right) + sum(node * 2 + 1, mid +1 , end, left, right);
}
5. 관련 알고리즘 문제
6. 마치며…
이번시간에는 구간합 및 특정 구간에서의 최대/최소를 구하는데에 대한 최적화 알고리즘인 인덱스트리(세그먼트트리)에 대해서 정리를 해보았습니다. 알고리즘을 공부하면 할 수록 이러한 자료구조에 대한 기본지식이 탄탄해야 된다는 것을 다시한번 느끼게 되었습니다.
세그먼트 트리를 활용해서 구할 수 있는 문제들에 대해서 좀 더 정리가 필요해보입니다. 관련 알고리즘 문제는 반드시 이해하고 풀이를 다시한번 해야된다는 것을 느끼게 되는 포스팅이였습니다.
다음시간에는 LCA에 대해서 정리를 해보도록 하겠습니다.
