[Algorithms] 벨만-포드 알고리즘
[Algorithms] 벨만-포드 알고리즘
안녕하세요? 정리하는 개발자 워니즈입니다. 이번시간에는 최단거리 알고리즘중 음의 가중치도 계산이 가능한 벨만-포드 알고리즘에 대해서 정리를 해보도록 하겠습니다. 다익스트라보다 시간 복잡도가 높기에 어떤 상황에서 이용해야 할지 잘 생각하여 사용해야합니다.
1. 벨만포드 기본 개념
최단 경로를 구하기 위해서는 다음과 같이 분해를 할 수 있습니다.
D(s, v) = D(s, u) + w(u, v)
즉, s->v로 가는 최단 거리는 s에서 u를 거치는 최단거리에서, u->v로 가는 간선의 정보를 합산한 거리가 최단거리가 된다는 이론입니다. s->u까지의 최단 경로를 구하기 위해서는 그래프내에 모든 노드들에 대해서 거리를 계산해야합니다.
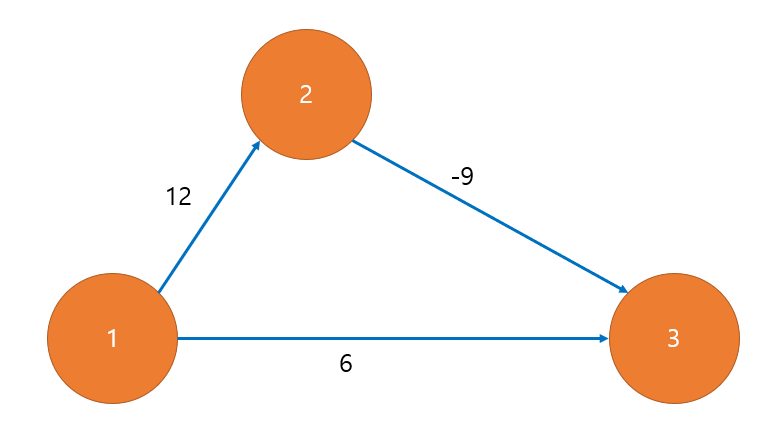
위의 그림에서 보면, 1에서 3으로 가는 최단거리를 구하는것을 생각해 봅시다. 1->3으로 가는것을 다익스트라로 구하게 되면, dist[3] = 6을 입력하고 종료하게 됩니다. 이유는 우선순위 큐에 간선정보가 들어가게 되면, 최단 거리인 6이 입력되고, 해당 값을 사용하면서 종료하게 됩니다. 모든값들이 양수라고 생각하고 설계된 알고리즘입니다. 즉, 12, 6중에서 6을 택한것이 다른 어떠한 값보다 더 최단이 된다고 생각하는 알고리즘입니다.
이전 포스팅에서 기록했지만, 음수에 대한 설계가 되어있지 않습니다. 벨만포드 알고리즘은 1->3으로 가는 모든 사이의 정점에 대해서 조사를 해보자라는 내용입니다. 즉, 최대 갖을 수 있는 숫자인 정점 빼기 1한 만큼의 iteration을 수행하면서 edge relaxation 을 수행하는 알고리즘입니다.
위에서 보면, 2번의 작업을 수행하게 됩니다. 먼저 정점 1번에서 출발하게 되면, dist[2] = 12, dist[3] = 6으로 업데이트를 수행합니다. 그 이후에, 2번 정점에서 출발하게 되고, dist[2] + (-9)를 하게 되면서, dist[3] = 3으로 업데이트를 수행하게 됩니다. 이것이 첫번쨰 iteration 의 종료입니다.
이런식으로 V-1번큼의 iteration을 돌면서 정점에 대해서 체크를 수행합니다.
2. 벨만-포드 예외사항
벨만포드 알고리즘은 위에서 보신바와 같이, 음수인 경우에도 적용 가능합니다. 그러나 다음과 같이 음수 가중치가 사이클(cycle)을 이루고 있는 경우에는 동작하지 않습니다. 아래의 그림에서 보면, c,d그리고 e,f가 사이클을 이루고 있는 것을 확인 할 수 있습니다. c,d의 경우에는 사이클을 돌아도 거리가 계속해서 커지지만, e,f같은 경우 사이클을 계속해서 돌게 되면, 음수 무한대로 커지게 됩니다.
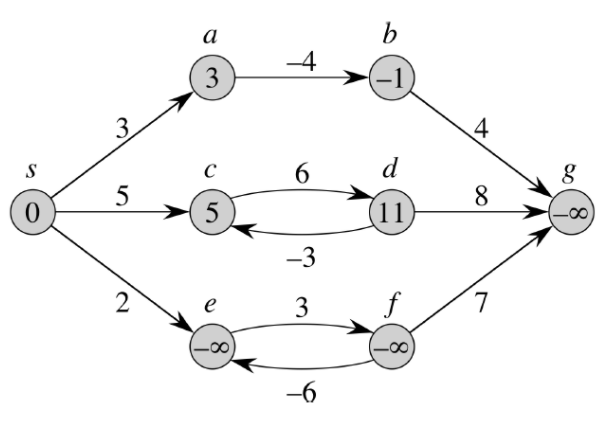
3. 벨만-포드 코드
우선순위큐 알고리즘과 다른 부분은 1개의 객체에 here, there, cost정보를 담고 있습니다.
static class Point{
// 시작점, 도착점, 걸리는 시간
int here, there, dist;
public Point(int here, int there, int dist){
this.here = here;
this.there = there;
this.dist = dist;
}
}
입력정보는 다음과 같이 받습니다. ArrayList를 따로 사용하지 않고, Point객체를 배열로 선언하여 담습니다.
// 2. 입력값 초기화
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int here = Integer.parseInt(st.nextToken());
int there = Integer.parseInt(st.nextToken());
int dist = Integer.parseInt(st.nextToken());
point[i] = new Point(here, there, dist);
}
실제 최단 거리를 구하는 수행은 아래의 벨만포드 함수로 작성했습니다. V-1 만큼의 최대간선수의 for문을 수행하고 아래의 내용은 각 정점으로부터 edge relaxation을 수행합니다.
private static boolean bellmanFord() {
dist[1] = 0;
// v - 1번 수행
for(int i = 1; i < n; i++){
// edge relaxtaion
for(int j = 0; j < m; j++){
Point p = point[j];
// dist[there] > 현재 정점 + 거리 이면, 최단으로 업데이트 수행
if(dist[p.here] != INF && dist[p.there] > dist[p.here] + p.dist){
dist[p.there] = dist[p.here] + p.dist;
}
}
}
}
위에서 보시는것이 벨만포드의 핵심 알고리즘 입니다. V-1 번만큼의 iteration을 돌면서 1회당 전체 edge에 대해서 relaxation을 수행합니다. 현재의 dist배열에 있는 값이 가려는 정점의 현재 dist배열의 값에 간선정보를 합산한것이 더 작으면 계속해서 dist배열을 업데이트 해줍니다. 이렇게 V-1번의 iteration만큼 진행하면, src정점으로부터 N번째 노드까지의 최단거리를 구하게 됩니다.
dist 배열의 가고자 하는 값이 dist배열의 현재 정점 + 거리를 합한 값보다 크다면 업데이트를 수행합니다.
4. 관련 알고리즘 문제
5. 마치며..
이번시간에는 음수의 간선에 대해서도 최단 거리를 계산이 가능한 벨만포드 알고리즘에 대해서 정리를 해보았습니다. 최단거리하면 다익스트라 알고리즘만 알고 있었는데, 벨만포드 알고리즘을 통해서도 src 정저으로부터 다른 정점에 대한 거리를 구하는 것이 가능합니다. 비록 다익스트라 알고리즘보다는 정점 * 간선의 갯수만큼 시간 복잡도가 나오므로, 좀더 시간이 걸린다는 단점이 있습니다. 하지만, 알고리즘 문제에서 음수의 간선이 나오면 고려를 해볼 수 있는 알고리즘 이라는 것을 알게 되었습니다.
다음시간에는 N개의 정점에서 다른 모든 정점으로의 거리를 구할 수 있는 플로이드-워셜 알고리즘에 대해서 정리를 해보도록 하겠습니다.
