[Algorithms] 최소 스패닝 트리(Minimum Spanning Tree)
[Algorithms] 최소 스패닝 트리(Minimum Spanning Tree)
안녕하세요? 정리하는 개발자 워니즈 입니다. 이번시간에는 지난시간에 이어서 최소 스패닝 트리에 대해서 정리를 해보려고 합니다.
1. 최소 스패닝 트리(Minimum Spanning Tree, MST)란?
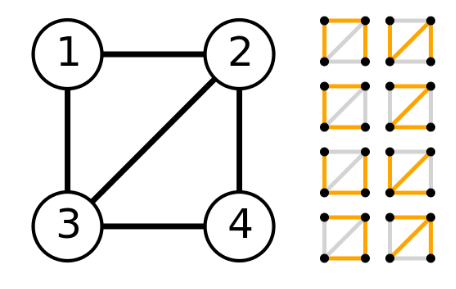
그래프의 모든 노드를 포함하고, 모든 노드가 서로 연결되어 있으면서 트리(Tree)의 속성을 만족하는 그래프를 가리킵니다. 예를들어 하단 좌측과 같은 원 그래프의 스패닝 트리는 하단 우측과 같이 총 8개의 스패닝 트리들을 가질 수 있습니다.
최소 신장 트리(MST)는 가능한 신장트리 가운데 엣지 가중치의 합이 최소인 신장트리를 말합니다. 예를들어 하단 좌측과 같은 원 그래프의 MST는 하단 우측과 같습니다 .
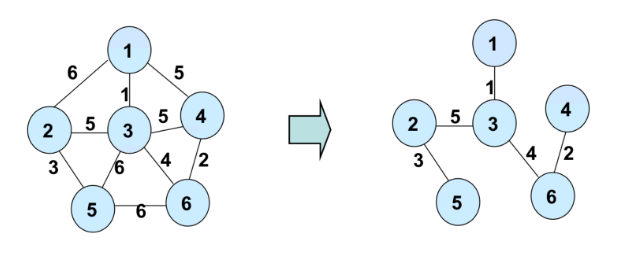
MST는 노드 간 연결성을 보장하면서 노드 사이를 잇는 거리/비용 등을 최소로 하는 그래프를 의미하기 떄문에 응용 범위가 넓습니다.
2. 크루스칼 알고리즘
크루스칼 알고리즘은 모든 간선에 대해 가장 가중치가 작은 간선부터 연결해주면서 최소 스패닝 트리를 만들어 나가는 알고리즘을 의미합니다.
이때 가장 작은 간선부터 간선을 연결하되, 연결하는 도중 사이클이 생기게 되면 가중치가 작은 간선이어도 무시하여야 합니다.
크루스칼 알고리즘은 Disjoint set을 기본 자료구조로 활용합니다.
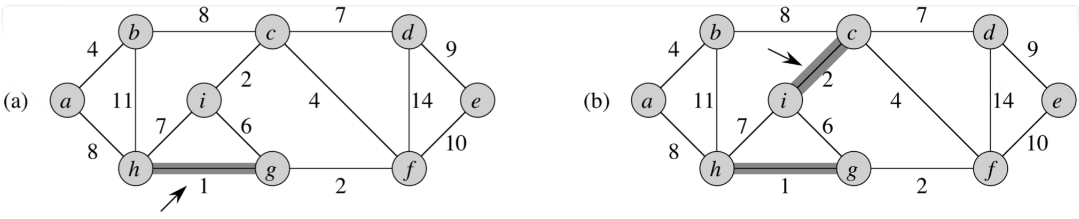
예를들어, 하단의 (a)를 보겠습니다. 그래프 모든 엣지 가운데 가중치가 최소 (1)인 (h,g)를 union 하게 됩니다. 해당 부분에는 cycle이 형성되어있지 않기 때문에 연결을 하게 되고, 가중치를 합산합니다.
(b)를 보게되면, 간선의 크기가 2번째인 (i,c)를 연결하게 됩니다.
(c)에서 간선의 크기가 (2)인 값을 계속해서 연결하게 됩니다. 연결되는 와중에는 union-find를 활용하여 같은 그룹으로 연결되어있는지를 체크합니다. 즉, cycle여부를 체크하게 됩니다.
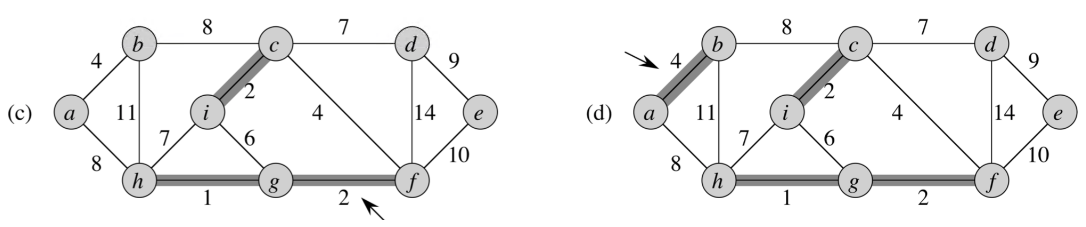
계속해서 연결을 하다가, (f)의 그립을 보게되면, 간선의 크기가 (6)인값을 연결을 수행하였고, (i,g,f,c)가 같은 그룹으로 연결되어 싸이클을 형성하게 되기때문에, 간선 (i,g)값의 연결을 포기하고 다음으로 넘어가게 됩니다.

위와 같은 방식으로 연결을 계속해서 수행하게 되면, (n)같은 그림이 도출이 됩니다.
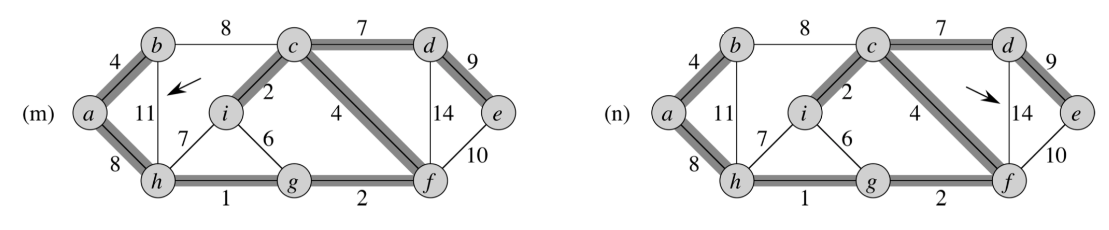
모든 정점의 노드가 간선으로 연결이 되어있고, 싸이클을 형성하지 않으면서 동시에 가장 최소의 간선합산으로 연결이 되어있습니다. 이것이 바로 MST이면서 동시에 크루스칼 알고리즘입니다 .
3. 관련 알고리즘 문제
가장 기본적인 MST 문제인거 같습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class MST_1197 {
static Vector edge;
static int n,m; // 3, 3
static int res;
static boolean chk;
static int[] parent;
//크루스칼 객체 (정점에 정보를 저장하는 객체)
static class kruscal{
int from, to, val;
public kruscal(int from, int to, int val) {
this.from = from;
this.to = to;
this.val = val;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
parent = new int[n+1];
for (int i = 1; i <= n; i++)
parent[i] = i;
//1. 그래프 형성
edge = new Vector();
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
kruscal ks = new kruscal(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
edge.add(ks);
}
Collections.sort(edge, new Comparator() {
@Override
public int compare(kruscal o1, kruscal o2) {
if(o1.val < o2.val) return -1;
else if(o1.val == o2.val) return 0;
else return 1;
}
});
///////////////////////////////////////////////////////////////////////
//2. 실제 작업.
for (int i = 0; i < m; i++) {
merge(edge.get(i).from, edge.get(i).to);
if(chk)
res += edge.get(i).val;
}
System.out.println(res);
}
public static int find(int u){
if(u == parent[u])
return u;
return parent[u] = find(parent[u]);
}
public static void merge(int u, int v){
chk = false;
u = find(u);
v = find(v);
if(u==v) return;
parent[u] = v;
chk = true;
}
}
중요한것은, vector안에 정점들의 값(from, to , val)순서로 넣고 value에 따라서 정렬을 수행합니다. 그리고 이어서 정점들을 하나씩 merge하되, 함수안에 내용을 보면 chk라는 같은 정점이면 거짓을 다른 정점이면 참으로 셋팅을 하도록 했습니다.
그래서 다른정점에 대한 간선값만 합산을 수행해서 최종적으로 res값을 출력해주는 문제입니다.
4. 마치며...
이번에는 최소 스패닝 트리에 대해서 알아보았습니다. 최소 스패닝 트리에는 크루스칼 외에도 프림 알고리즘이 있습니다. 이부분을 정리하기 위해서는 다익스트라에 대한 정리를 먼저 한 뒤, 이번 포스팅을 업데이트 하는 순서로 진행을 하고자 합니다.
다음시간에는 알고리즘에서 필수항목인 자료구조에 대해서 정리를 해보도록 하겠습니다.
